Define recurrence relation. What do you mean by linear homogeneous recurrence of degree \( k \) with constant coefficients? What is the solution of the recurrence relation \( a_n = a_{n-1} + a_{n-2} \) with initial conditions \( a_0 = 0 \) and \( a_1 = 1 \)? [10]

Differentiate permutation with combination. What is the next permutation in lexicographic order after 362541? [5]

Explain mathematical induction. Use mathematical induction to prove that the sum of the first n odd positive integers is $n^2$. What is recursively defined function? [10]

What do you mean by converse, inverse, and contrapositive? Show that the sentences "if it is hot today then today is Sunday" and "if it is not Sunday then today is not hot" are logically equivalent. [5]

What direct proof? Give a direct proof of the theorem "If n is an odd integer, then $n^2$ is an odd integer." [5]

Explain Euclidean algorithm. Use Euclidean algorithm to find the greatest common divisor of 414 and 662. [5]

Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Use bit strings to find the union and intersection of the sets {1, 2, 3, 4, 5} and {1, 3, 5, 7, 9}. [5]

Define celling and floor function. Explain Boolean function with example. [5]

How can we represent a relation using directed graph? Draw a directed graph of the relation R = {(1, 1), (1, 3), (2, 1), (2, 3), (2, 4), (3, 1), (3, 2), (4, 1)} on the set {1, 2, 3, 4}. [5]

What is shortest path finding problem? Use Dijkstra's algorithm to find the length of the shortest path between a and z in the given weighted graphs. 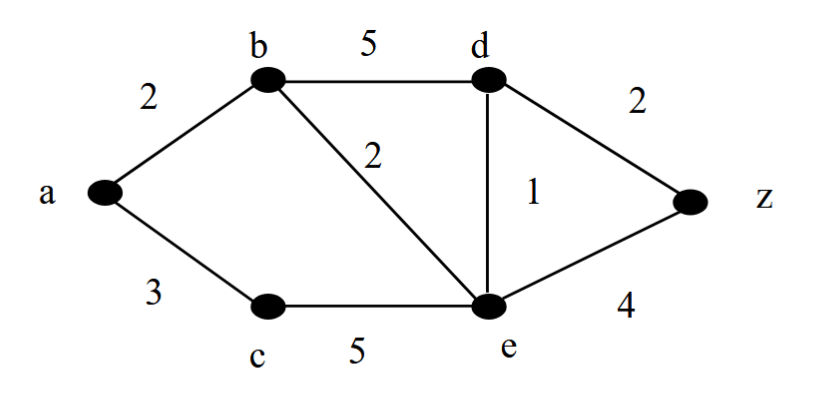[10]

How can we represent a graph using Adjacency Matrix? Explain. [5]

Define spanning tree. Explain minimum spanning tree with example. [5]