What is linear nonhomogeneous recurrence relation of degree k with constant coefficients? Find all the solutions of the recurrence relation a, 4a+n. Also find the solution of the relation with initial condition a, 1. [10]

Explain product rule. How many strings are there of four lowercase letters that have the letter x in them? [5]

Use mathematical induction to show that the sum of first n positive integers is n(n+1)/2. [5]

Explain direct proof, indirect proof, and proof by contradiction. Use direct proof to show that 'If n is an odd integer, then n' is an odd integer'. Also use indirect proof to show that 'If n is an integer and n' then n is odd'. [10]

What is tautology? Show $(p \land q) \rightarrow (p \lor q)$ is a tautology. [5]

What is congruent modulo? Determine whether 20 is congruent to 8 modulo 6 and 25 is congruent to 17 modulo 5. [5]

Explain trial division with example? Using trial division, show that 101 is prime. [5]

Define cartesian product. Find A3 for the set A = (a, b, c). [5]

How can you represent relations using matrices? Suppose that $A = \{1,\,2,\,3\}$ and $B = \{1,\,2\}$. Let $R$ be the relation from $A$ to $B$ containing $(a,\,b)$ if $a \in A$, $b \in B$, and $a > b$. What matrix representing $R$ if $a_1 = 1$, $a_2 = 2$, $a_3 = 3$, and $b_1 = 1$ and $b_2 = 2$? [5]

Define spanning tree and minimum spanning tree with suitable example. Use Kruskal's algorithms to find minimum spanning tree in the given graph 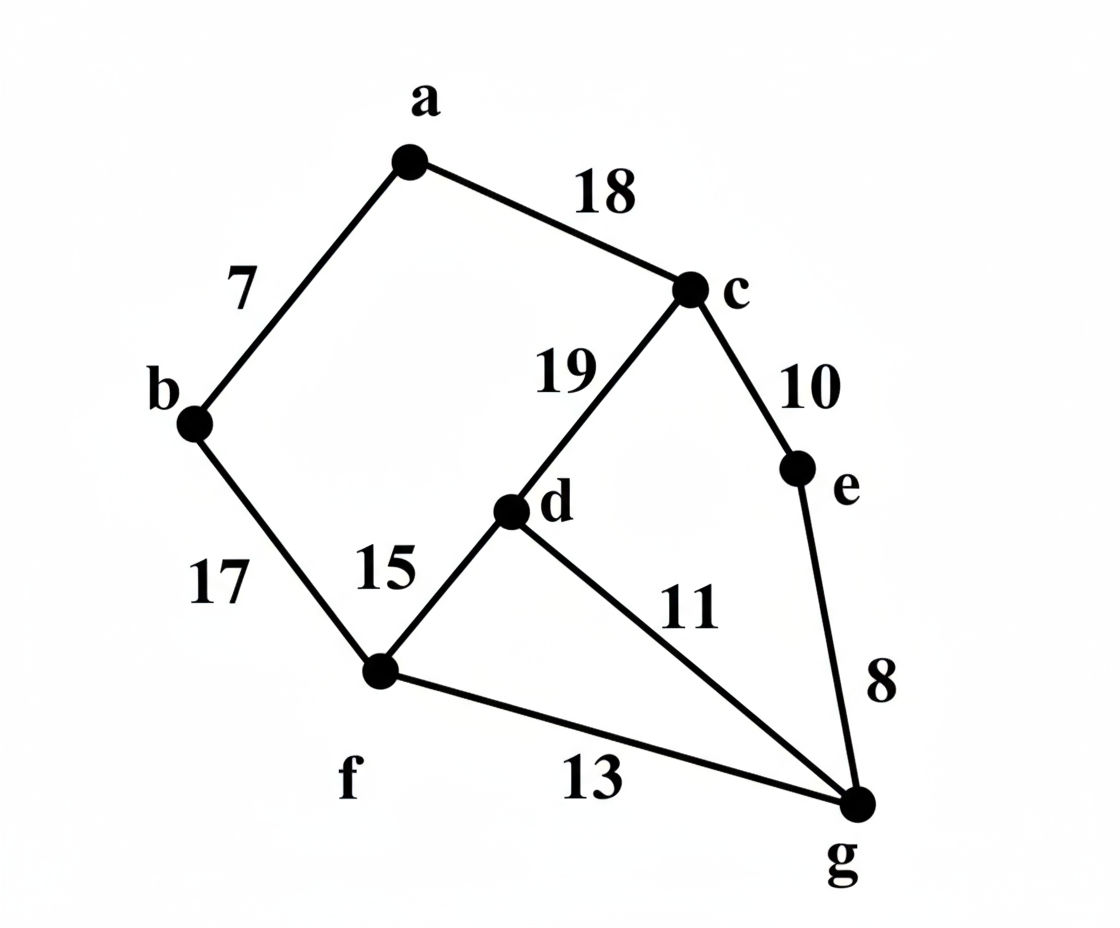[10]

What is graph? Explain simple graph and pseudograph with example. [5]

What is Euler path? Compare it with Hamilton path. [5]