Semester
Subject
Year
B.Sc Computer Science and Information Technology
Institute of Science and Technology, TU
Theory of Computation (CSC262)
Year Asked: 2080, syllabus wise question
Basic Foundations
1.
Define string, substring, empty string, and empty language over alphabet {a,b}. [5]
2.
How abstract, decision and optimization problems are different from each other? [5]
Context Free Grammar
1.
Define context free grammar with an example. Explain with example, how context free grammar is converted to Chomsky Normal Form. [10]
2.
What is the meaning of the term 'Context Free' in context free grammar? Justify with a suitable example. What is the need of a parse tree? [5]
Introduction to Finite Automata
1.
What is NFA? How is it different from DFA? How is NFA to DFA conversion done? Convert the following NFA into DFA. 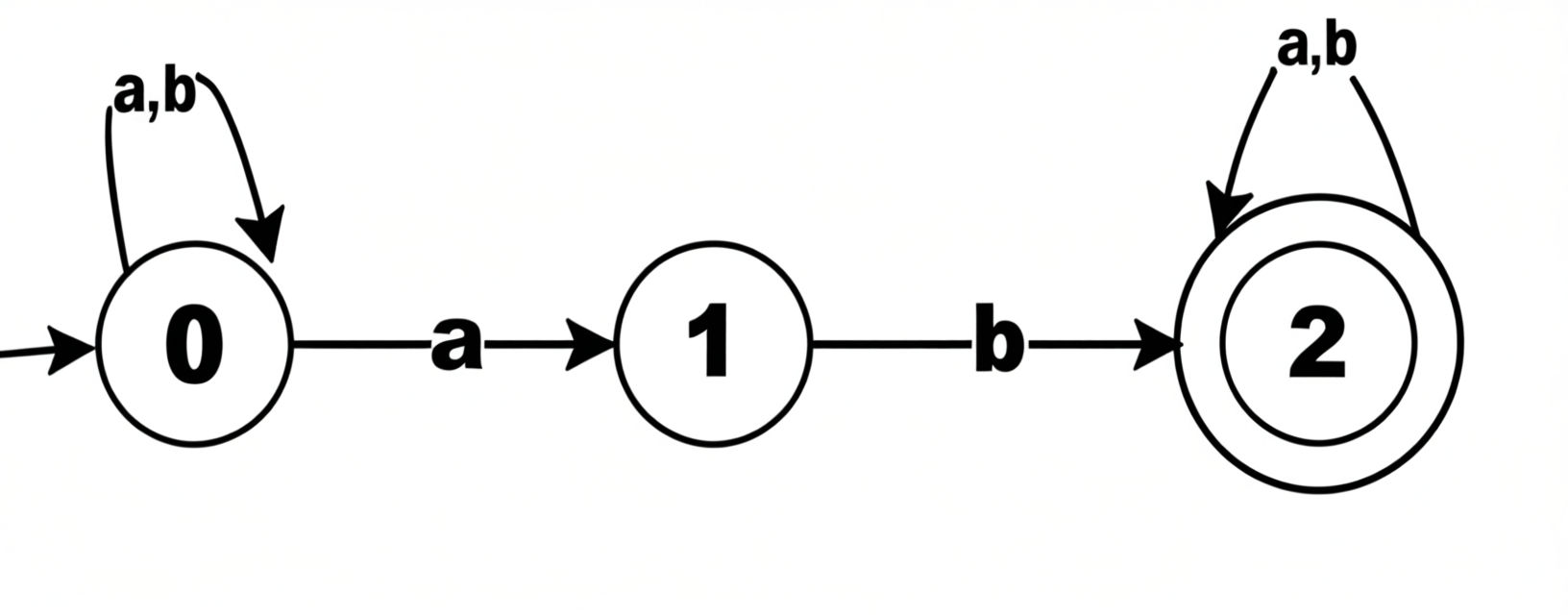 [10]
[10]

2.
Design a DFA that accepts single line and multi-line comments of the C-Language. [5]
Push Down Automata
1.
Design a PDA over {x,y} which accepts strings defined by the language Show acceptance of xxyy.
[5]
2.
How is PDA to CFG conversion done? Consider a PDA that accepts by empty stack, Now construct an equivalent CFG.
[5]
Regular Expressions
1.
Write regular expression over {a,b} that represents a. Strings having exactly two a's and at least two b's. b. Strings having an even number of a's and each a followed by at least one b. [5]
2.
Using pumping lemma, prove that the language is not regular.
[5]
Turing Machines
1.
How does Turing machine accept a string? Design a Turing Machine over the alphabet {0,1,a} that processes the string defined by L = {a01a,a10a,a0101a}. Show both transition diagram and table. Show acceptance of a0101a. [10]
2.
Design a Turing machine that computes a function f(n)=0. [5]