Questions
Syllabus
Qns. By Syllabus

Semester

Subject

Year

Bachelors Level/Second Year/Fourth Semester/Science csit/fourth semester/theory of computation/syllabus wise questions

B.Sc Computer Science and Information Technology

Institute of Science and Technology, TU

Theory of Computation (CSC262)

Year Asked: 2081, syllabus wise question

Basic Foundations
1.
Does machine always refer to hardware? Justify. Define positive closure and Kleene closure. [5]
2.
Define ε\varepsilon-closure of a state. Differentiate between Moore and Mealy machine. [5]
Context Free Grammar
1.
Define the language of a grammar. For the grammar , show the leftmost derivation for the string 00100 with its parse tree.
S→0S0∣1∣εS \rightarrow 0S0 \mid 1 \mid \varepsilon
[5]
2.
Convert the following grammar to CNF.
S→AAB,A→aA∣ε,B→ab∣aS \rightarrow AAB, \quad A \rightarrow aA \mid \varepsilon, \quad B \rightarrow ab \mid a
[5]
Introduction to Finite Automata
1.
Design the DFA that accepts binary string ending with '00' and show its extended transition function for the string 111000. [5]
Push Down Automata
1.
Mention the transition function of PDA. List the two ways that PDA accepts the string. Convert the following CFG to PDA.
S→AS∣εS \rightarrow AS \mid \varepsilon
A→Ab∣Bb∣abA \rightarrow Ab \mid Bb \mid ab
[10]
Regular Expressions
1.
List any two regular operators. Minimize the following finite state machine using Table Filling algorithm.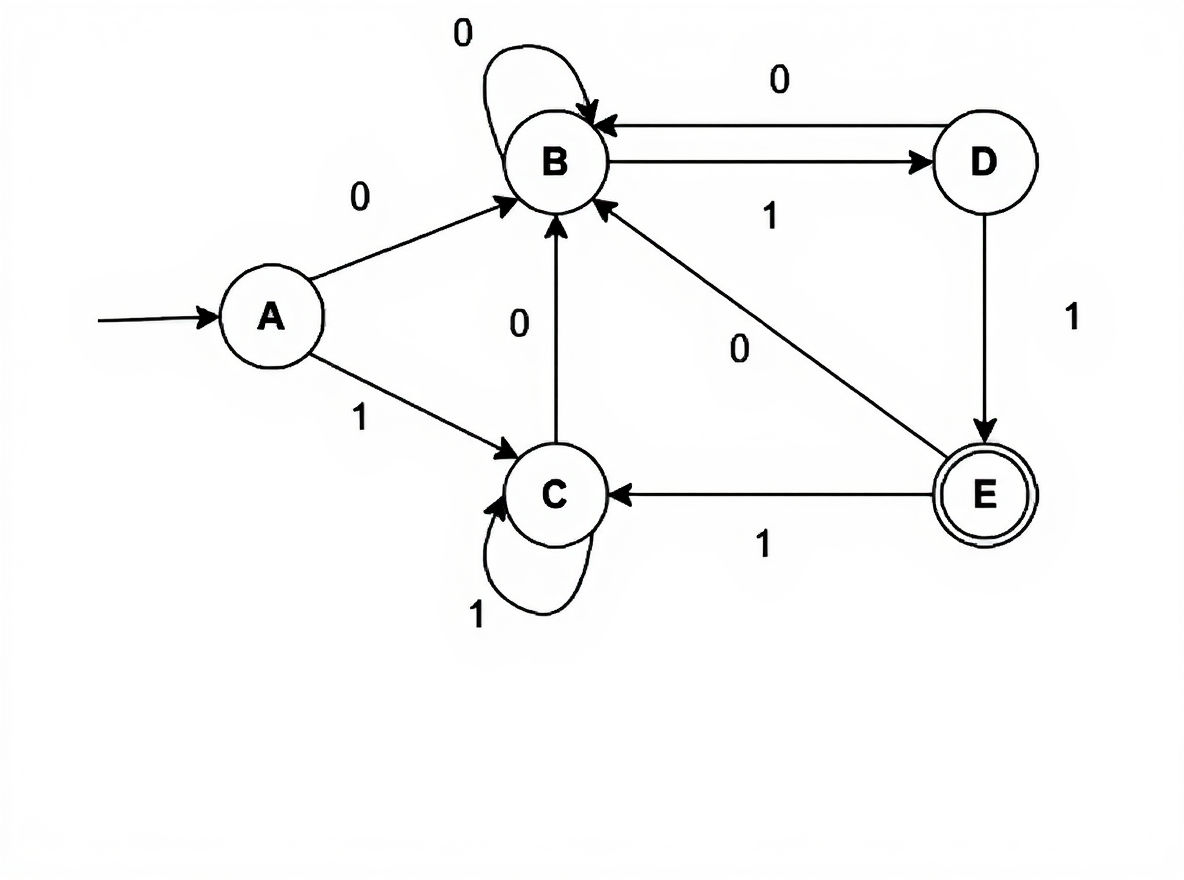
question image
[10]
2.
Represent the following regular grammar to finite automata.
S→aA∣aB∣εS \rightarrow aA \mid aB \mid \varepsilon
A→aA∣aSA \rightarrow aA \mid aS
B→bB∣εB \rightarrow bB \mid \varepsilon
[5]
Turing Machines
1.
Define Turing machine as enumerators of strings of a language. Encode the Turing machine TM = ({q0, q1, q2}, {a, b}, {a, b, B}, δ, q2, B, F) with input w = ba and δ is defined as follows: δ(q0, b) → (q1, b, R), δ(q1, a) → (q2, a, R), δ(q2, a) → (q1, a, R), δ(q2, b) → (q2, b, L) [10]
2.
For the following Turing Machine, test whether the string “())))” is accepted or rejected and represent it in transition diagram.
StateXAction (Write, Move, New State)YAction (Write, Move, New State)BAction (Write, Move, New State)q0(X,R,q1,,q0,,q4q1)X,L,q2Y,L,q2Y,L,q2q2XX,R,q0YY,R,q3,R,q4q3(,,q3,,q3,R,q4\begin{array}{|c|c|c|c|c|c|c|} \hline \text{State} & X & \text{Action (Write, Move, New State)} & Y & \text{Action (Write, Move, New State)} & B & \text{Action (Write, Move, New State)} \\ \hline q_0 & ( & X,R,q_1 & & , ,q_0 & & , ,q_4 \\ q_1 & ) & X,L,q_2 & & Y,L,q_2 & & Y,L,q_2 \\ q_2 & X & X,R,q_0 & Y & Y,R,q_3 & & ,R,q_4 \\ q_3 & ( & , ,q_3 & & , ,q_3 & & ,R,q_4 \\ \hline \end{array}
[5]
Undecidability and Intractability
1.
What is undecidable problem? Discuss about Post Correspondence Problem. [5]
2.
Differentiate between Class P and Class NP problem. Mention the transition function of DFA, NFA, and ε-NFA. [5]