Semester
Subject
Year
Tribhuwan University
Institute of Science and Technology
2079
Bachelor Level / Third Year / Fifth Semester / Science
B.Sc in Computer Science and Information Technology (CSC325)
(Design and Analysis of Algorithms)
Full Marks: 60
Pass Marks: 24
Time: 3 Hours
Candidates are required to give their answers in their own words as for as practicable.
The figures in the margin indicate full marks.
Section A
Long Answers Questions
Attempt any TWO questions.
[2*10=20]
1.
Explain the divide and conquer strategy for problem solving. Describe the worst-case linear time selection algorithm and analyze its complexity.[10]
2.
Write the dynamic programming algorithm for matrix chain multiplication. Find the optimal parenthesization for the matrix chain product $ABCD$ with size of each is given as $A_{5\times10}, B_{10\times15}, C_{15\times20}, D_{20\times30}$.[10]
3.
What do you mean by Backtracking? Explain the backtracking algorithm for solving knapsack problem and find the solution for the problem given below and capacity of knapsack is 10 kg
$\begin{bmatrix} \text{Items} & 1 & 2 & 3 & 4 \\ \text{Weight (w}_i\text{)} & 2 & 3 & 4 & 5 \\ \text{Profit (P}_i\text{)} & 3 & 5 & 6 & 10 \end{bmatrix}$
[10]
$\begin{bmatrix} \text{Items} & 1 & 2 & 3 & 4 \\ \text{Weight (w}_i\text{)} & 2 & 3 & 4 & 5 \\ \text{Profit (P}_i\text{)} & 3 & 5 & 6 & 10 \end{bmatrix}$
Section B
Short Answers Questions
Attempt any Eight questions.
[8*5=40]
4.
Generate the prefix code for the string "CYBER CRIME" using Huffman algorithm and find the total number of bits required. [5]
5.
Find the edit distance between the string "ARTIFICIAL" and "NATURAL" Using dynamic programming. [5]
6.
Write short notes on: a) Best, Worst and average case complexity b) Greedy Strategy [5]
7.
Solve the following recurrence relations using masters method.
$\text{a. } T(n) = 2T(n/4) + kn^2,\ n > 1;\ T(1) = 1$
$\text{b. } T(n) = 5T(n/4) + kn,\ n > 1;\ T(1) = 1$ [5]
$\text{a. } T(n) = 2T(n/4) + kn^2,\ n > 1;\ T(1) = 1$
$\text{b. } T(n) = 5T(n/4) + kn,\ n > 1;\ T(1) = 1$
8.
Solve the following linear congruences using Chinese Remainder Theorem.$x \equiv 1 \pmod{2},\quad x \equiv 3 \pmod{5},\quad x \equiv 6 \pmod{7}$ [5]
9.
Find the MST from following graph using Kruskal's algorithm.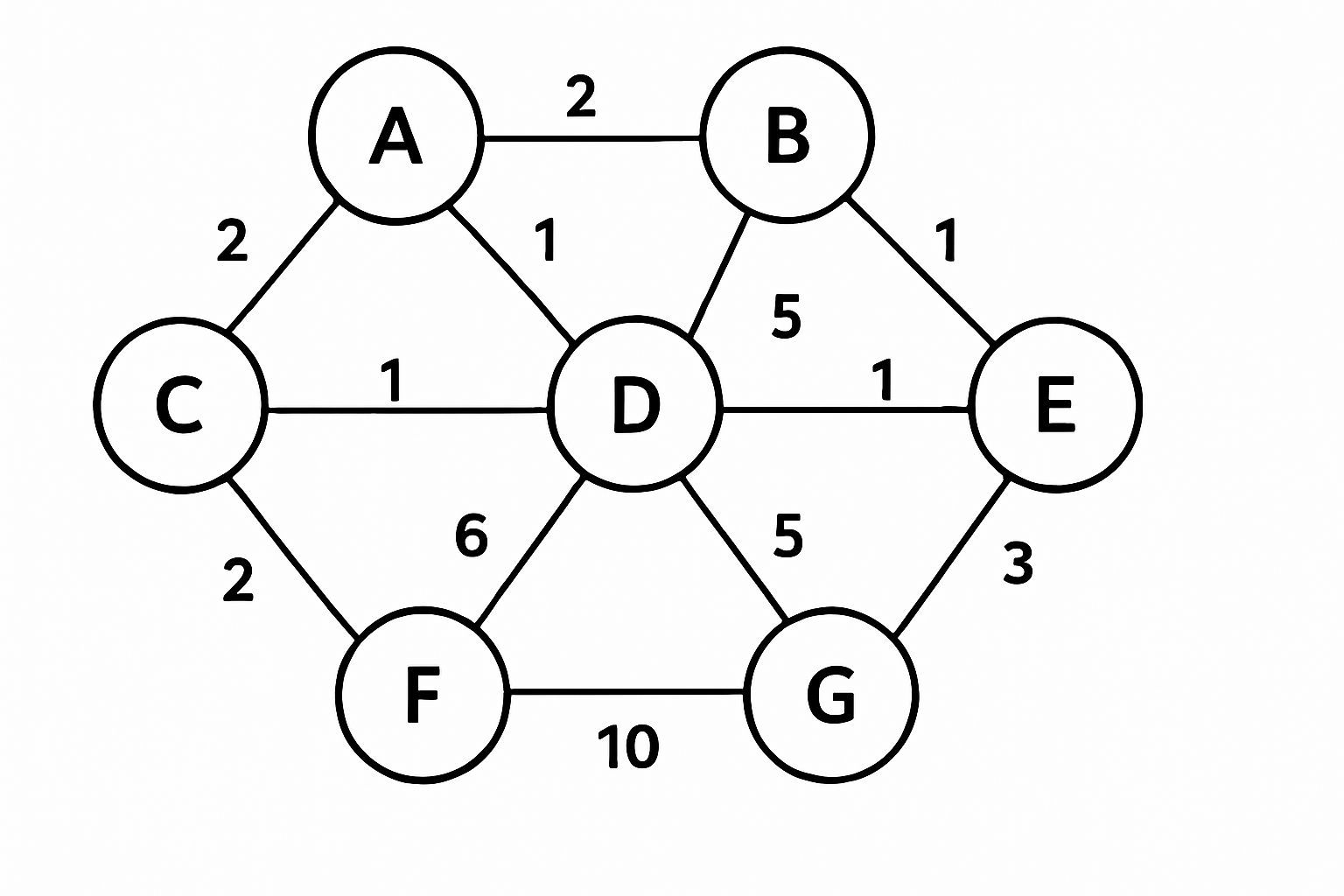
[5]
10.
Trace the quick sort algorithm for sorting the array $A[] = \{15,7,6,23,18,34,25\}$ and write its best and worst complexity. [5]
11.
Explain the iterative algorithm to find the GCD of given two numbers and analyze its complexity. [5]
12.
Define tractable and intractable problem. Illustrate vertex cover problem with an example. [5]