Semester
Subject
Year
Tribhuwan University
Institute of Science and Technology
2081
Bachelor Level / Third Year / Fifth Semester / Science
B.Sc in Computer Science and Information Technology (CSC325)
(Design and Analysis of Algorithms)
Full Marks: 60
Pass Marks: 24
Time: 3 Hours
Candidates are required to give their answers in their own words as for as practicable.
The figures in the margin indicate full marks.
Section A
Long Answers Questions
Attempt any TWO questions.
[2*10=20]
1.
Differentiate between dynamic programming and memorization. Compute the shortest path between every pairs in the following graphs using Floyd Warshall algorithm.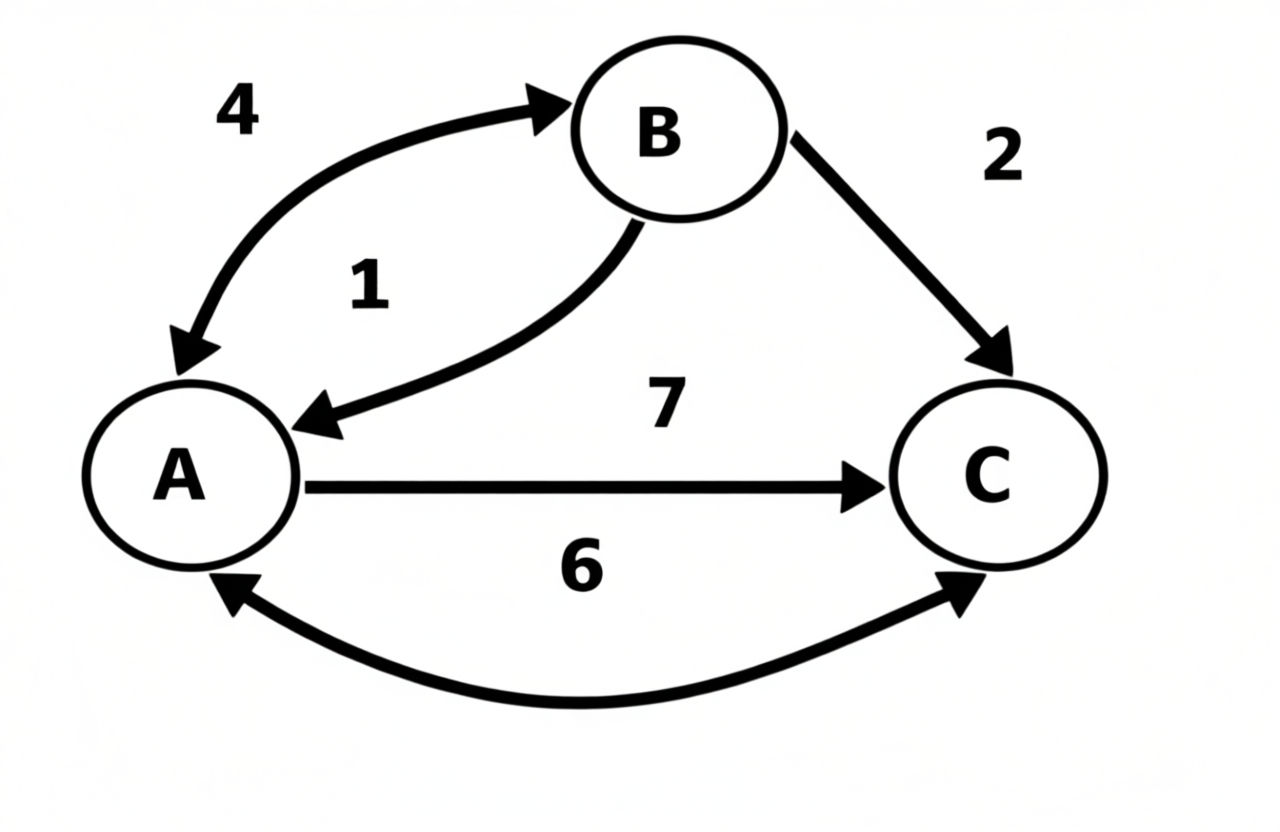
[10]
2.
What is the worst case of quick sort and how does randomize quick sort handle this problem? Sort the data $\{-2,4,-3,6,12,10,11,13,9\}$ using quick sort.[10]
3.
Does greedy algorithm guarantee optimal solution? Solve the Fractional knapsack problem to find maximum loot from given information.
$\begin{array}{|c|c|c|c|c|c|c|c|}\hline \text{Item} & 1 & 2 & 3 & 4 & 5 & 6 & 7 \\ \hline \text{Value} & 12 & 10 & 20 & 15 & 2 & 3 & 50 \\ \hline \text{Weight (kgs)} & 2 & 1 & 3 & 2 & 12 & 10 & 1 \\ \hline \end{array}$
[10]
$\begin{array}{|c|c|c|c|c|c|c|c|}\hline \text{Item} & 1 & 2 & 3 & 4 & 5 & 6 & 7 \\ \hline \text{Value} & 12 & 10 & 20 & 15 & 2 & 3 & 50 \\ \hline \text{Weight (kgs)} & 2 & 1 & 3 & 2 & 12 & 10 & 1 \\ \hline \end{array}$
Section B
Short Answers Questions
Attempt any Eight questions.
[8*5=40]
4.
Given a set $A=\{5,7,10,12,15,18,20\}$, find the subset that sum to 35 using backtracking. [5]
5.
Solve the following recurrence relations using master's method.
$T(n) = 2T\left(\frac{n}{2}\right) + n^3,\ n > 1;\quad T(n) = 1,\ n = 1$
$T(n) = 2T\left(\frac{n}{4}\right) + 1,\ n > 1;\quad T(n) = 1,\ n = 1$ [5]
$T(n) = 2T\left(\frac{n}{2}\right) + n^3,\ n > 1;\quad T(n) = 1,\ n = 1$
$T(n) = 2T\left(\frac{n}{4}\right) + 1,\ n > 1;\quad T(n) = 1,\ n = 1$
6.
Define order statistics problem. Find the edit distance between 'cat' and 'car' using dynamic programming. [5]
7.
Discuss about recursion and backtracking. Analyze the complexity of Miller Rabin Randomized Primality test. [5]
8.
Solve the following linear equation using Chinese Remainder Theorem. x = 1 MOD 3,x = 2 MOD 5,x = 0 MOD 7 [5]
9.
Explain the approximation algorithm for vertex cover of a connected graph with an example. [5]
10.
State cooks theorem. Discuss about problem reducibility. [5]
11.
Write short notes on: a) Big Oh, Big Omega, Big theta b) Class P, Class NP and NP-Complete [5]
12.
Write an algorithm to find the $n^{th}$ fibonacci number with its time and space complexity. [5]