Semester
Subject
Year
Tribhuwan University
Institute of Science and Technology
2075
Bachelor Level / First Year / Second Semester / Science
B.Sc in Computer Science and Information Technology (CSC165)
(Discrete Structures)
Full Marks: 60
Pass Marks: 24
Time: 3 Hours
Candidates are required to give their answers in their own words as for as practicable.
The figures in the margin indicate full marks.
Section A
Long Answers Questions
Attempt any TWO questions.
[2*10=20]
1.
What is S-D cut? For the following network flow find the maximal flow from S to D. 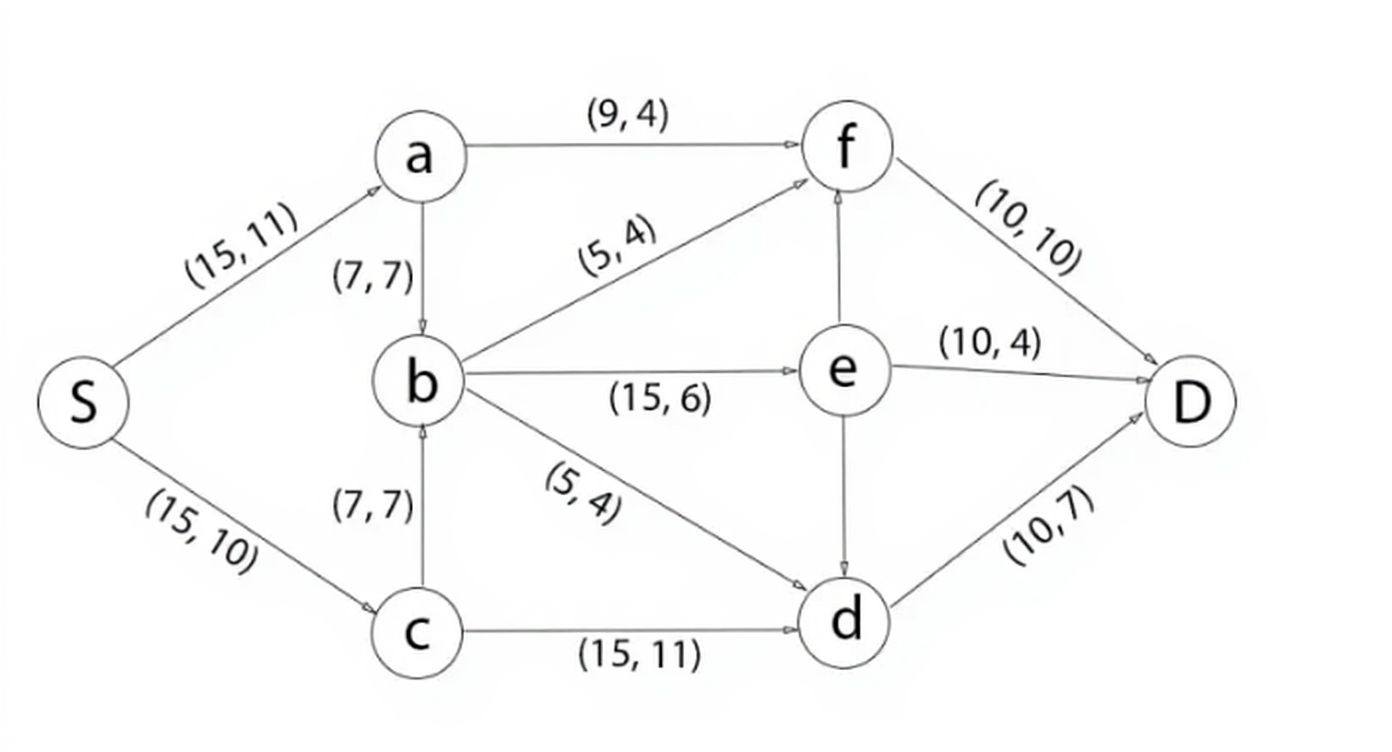 [10]
[10]

2.
Consider a set U = {1,2,3,4,5,6,7,8,9,10}. What will be the computer representation for set containing the numbers which are multiple of 3 not exceeding 6? Describe injective, surjective and bijective function with examples. [10]
3.
Compute the values. 3 mod 4 , 7 mod 5, -5 mod 3 , 11 mod 5 and -8 mod 6 Write down the recursive algorithm to find the value of and prove its correctness using induction. [5+5]
Section B
Short Answers Questions
Attempt any Eight questions.
[8*5=40]
4.
Solve the recurrence relation , with initial conditions and . [5]
5.
Find the values of x such that x = 1 (mod 5) and x = 2 (mod 7) using Chinese remainder theorem. [5]
6.
Prove that is divisible by 4 using mathematical induction. [5]
7.
Let A = 'Aldo is Italian' and B = 'Bob is English'. Formalize the following sentences into proposition.a. Aldo isn't Italian.b. Aldo is Italian while Bob is English.c. If Aldo is Italian then Bob is not English.d. Aldo is Italian or if Aldo isn't Italian then Bob is English.e. Either Aldo is Italian and Bob is English, or neither Aldo is Italian nor is Bob English. [5]
8.
Define Euler path and Hamilton path with examples. Draw the Hasse diagram for the divisibility relation on the set {1,2,5,8,16,32} and find the maximal, minimal, greatest and least element if exist. [5]
9.
What does probability testing means? Describe how Fermat's Little Theorem tests for a prime number with suitable example. [5]
10.
List any two applications of conditions of probability. You have 9 families you would like to incite to a wedding. Unfortunately, you can only invite 6 families. How many different sets of invitations could you write? [5]
11.
Define spanning tree and minimum spanning tree, mention the conditions for two graphs for being isomorphic with ean example [5]
12.
Prove that the product xy is odd if and only if both x and y are odd integers. [5]