Semester
Subject
Year
Tribhuwan University
Institute of Science and Technology
2079
Bachelor Level / First Year / Second Semester / Science
B.Sc in Computer Science and Information Technology (CSC165)
(Discrete Structures)
Full Marks: 60
Pass Marks: 24
Time: 3 Hours
Candidates are required to give their answers in their own words as for as practicable.
The figures in the margin indicate full marks.
Section A
Long Answers Questions
Attempt any TWO questions.
[2*10=20]
1.
How do you plot the function on graph? Determine whether the function is injective, surjective or bijective with reasons. Solve the recurrence relation with initial conditions . [10]
2.
A group of 8 scientist is composed of 5 chemist and 3 biologist. In how many ways can a committee of 5 be formed that has 3 chemist and 2 biologist? Using mathematical induction prove that for . [10]
3.
Show that the relation R = {(a, b): |a-b| is even} is an equivalence relation in the set of integers. Given the following transport network with the edges called with their capacities find all S-D cuts and their capacities and what the minimum capacity? 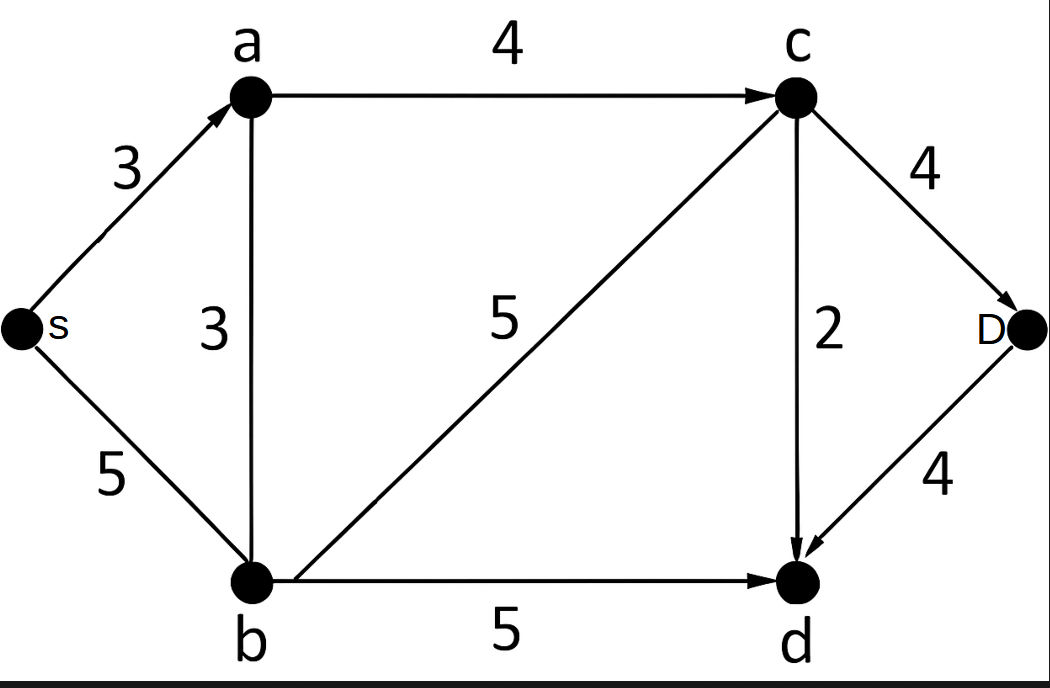 [10]
[10]

Section B
Short Answers Questions
Attempt any Eight questions.
[8*5=40]
4.
List any one example of tautology. Represent the following sentences into predicate logic. a. Not all employees are loyal. b. All students having good attitude are lovable. [5]
5.
Prove that 'If the product of two integers a and b is even then either a is even or b is even' using condition method. [5]
6.
Use Chinese remainder Theorem to find the value of x such that x = 0 (MOD 2), x = 2 (MOD 3), x = 3 (MOD 5). [5]
7.
Define bipartite graph with an example. State the necessary conditions for the graphs to be isomorphic. [5]
8.
State Generalized Pigeonhole principle. Find the MST from following graph using Kruskal Algorithm. 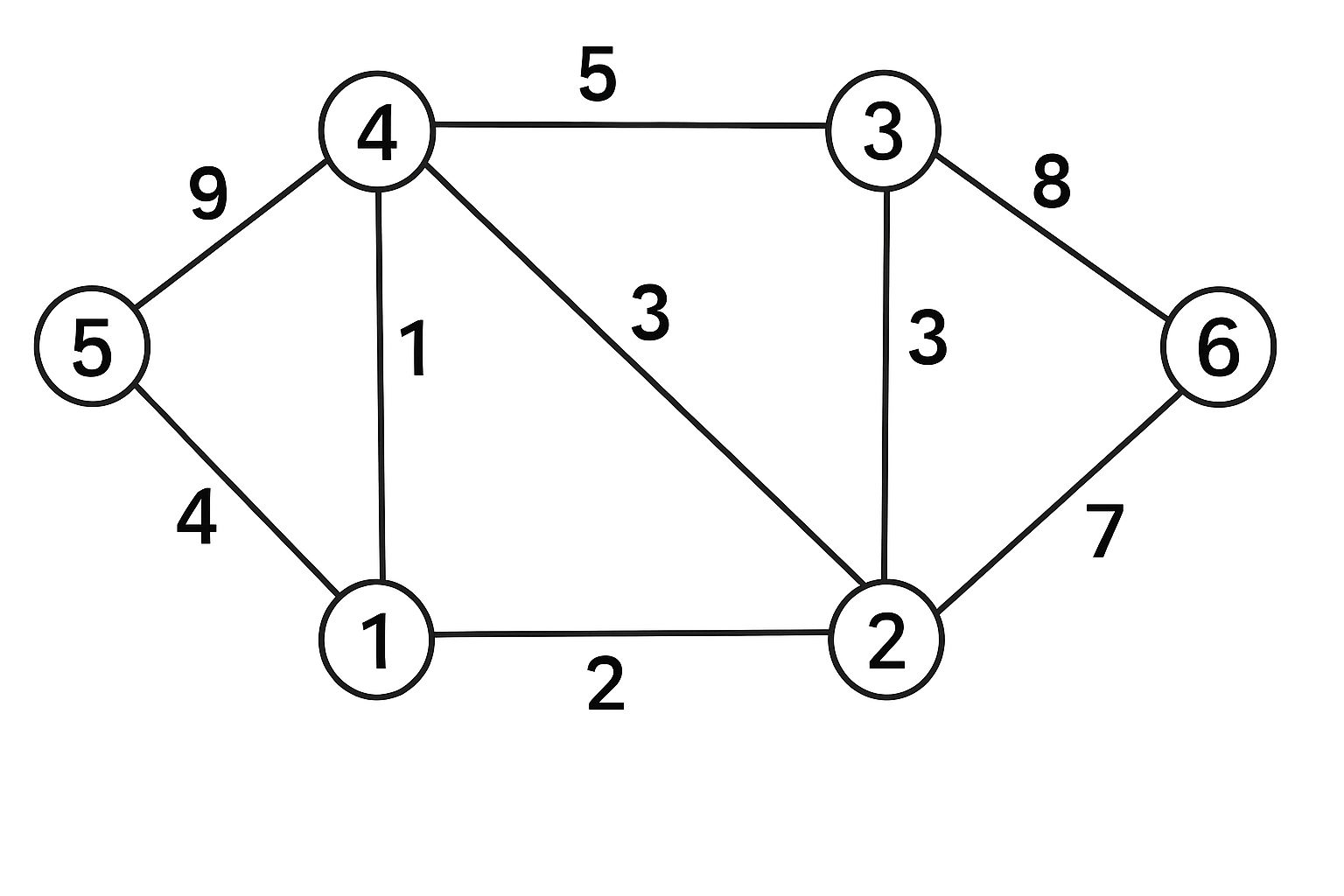 [5]
[5]

9.
Give the premise 'If it rains or strike holds then the exam will be cancelled. If it doesn't rain then it will be sunny day. The exam was not cancelled. Show that it was sunny day'. [5]
10.
Find the value of -2 MOD 3 and MOD 5. Illustrate an example to show the join operation between any two Boolean matrices. [5]
11.
Give an example of fallacy. State the necessary and sufficient conditions for a graph to have Euler path and Euler circuit. [5]
12.
Find the GCD of 24 and 32 using Extended Euclidean algorithm. [5]