What is the coefficient of $x^2$ in $(1 + x)^{11}$? Describe how relation can be represented using matrix. [5]

Show that if there are 30 students in a class, then at least two have same names that begin with the same letter. Explain the pascal's triangle. [5]

Represent any three set operations using Venn-diagram. Give a recursive defined function to find the factorial of any given positive integer. [5]

Prove that for all integers x and y, if $x^2 + y^2$ is even then x + y is even. Using induction prove that $1^3 + 2^3 + 3^3 + ... + n^3 = n^2(n + 1)^2/4$ [10]

Solve the recurrence relation $a_n = 5a_{n-1} - 6a_{n-2}$, with initial conditions $a_0 = 1$, $a_1 = 4$. [5]

Prove that if n is positive integer, then n is odd if and only if 5n + 6 is odd. [5]

Define zero-one matrix. Explain the types of function. [5]

State division and remainder algorithm. Suppose that the domain of the propositional function P(x) consists of the integer 0, 1, 2, 3 and 4. Write out each of the following propositions using disjunctions, conjunctions and negations. $\text{a. } \exists x \, P(x) \quad \text{b. } \forall x \, P(x) \quad \text{c. } \exists x \, \neg P(x) \quad \text{d. } \forall x \, \neg P(x) \quad \text{e. } \neg \exists x \, P(x) \quad \text{f. } \neg \forall x \, P(x)$ [10]

Define proposition. Consider the argument 'John, a student in this class knows how to write program in C. Everyone who knows how to write program in C can get a high paying job. Therefore, someone in this class can get high paying job'. Now, explain which rules of inferences are used for each step. [5]

List all the necessary conditions for the graph to be isomorphic with an example. Find the maximal flow from the node SOURCE to SINK in the following network flow. 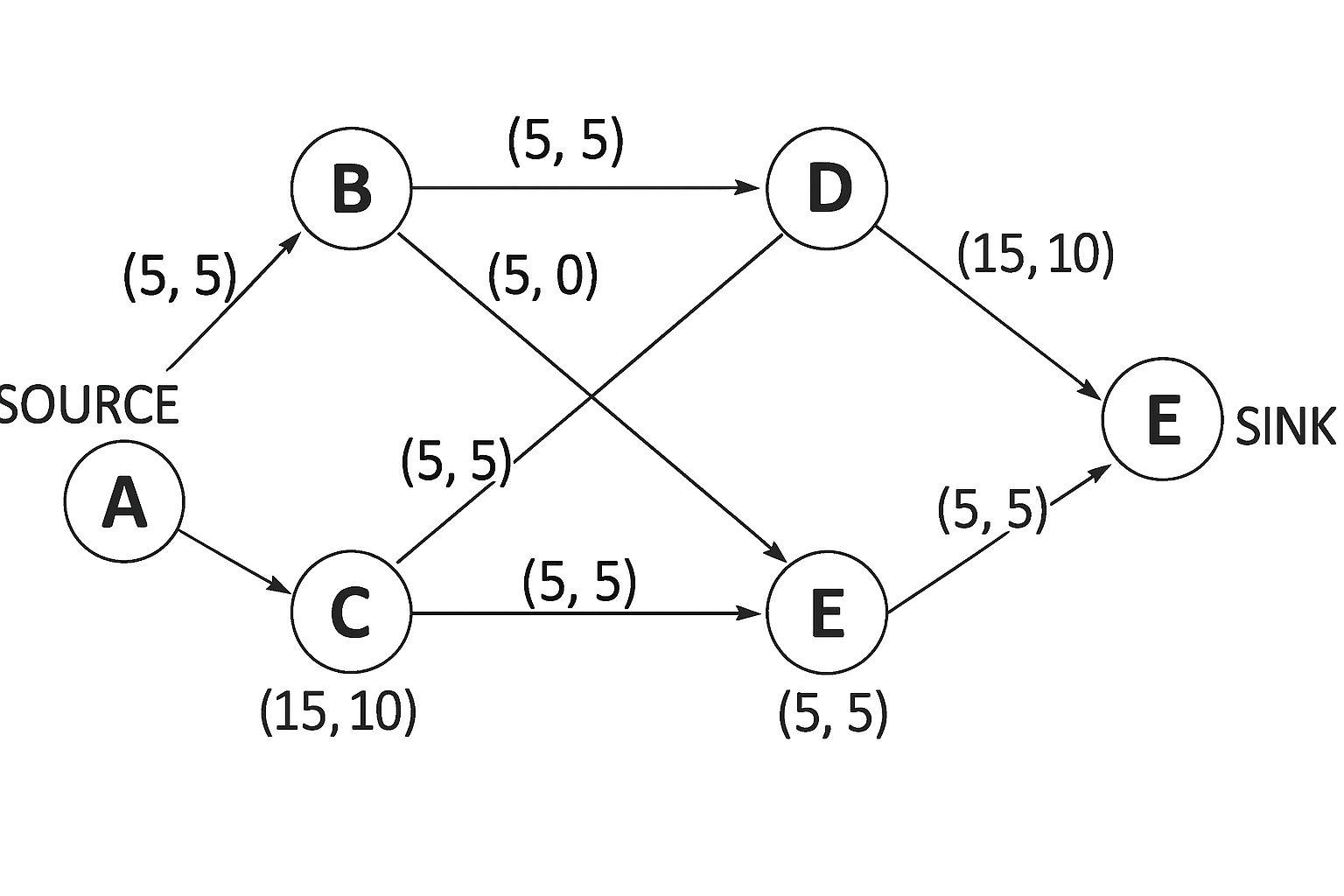[10]

Illustrate the Dijkstra's Algorithm to find the shortest path from source node to destination node with an example. [5]

What are the significance of Minimum Spanning Tree? Describe how Kruskal's algorithm can be used to find the MST. [5]