StudyNp | CSIT Second Semester – 2080.1 Question | Discrete Structures (Syllabus Wise)

Bachelors Level/First Year/Second Semester/Science csit/second semester/discrete structures/syllabus wise questions

Institute of Science and Technology, TU

Discrete Structures (CSC165)

Year Asked: 2080.1, syllabus wise question

Explain fuzzy set with example. How do you find complement of a fuzzy set? [5]

What is product rule? How many strings are there of four lowercase letters that have the letter x in them? [5]

How can you use mathematical induction to prove statements? Use mathematical induction to show that sum of first n positive integer is

\frac{n(n+1)}{2}

[10]

Explain linear homogeneous recurrence relation with constant coefficients. What is the solution of the recurrence relation

a_n = 6a_{n-1} - 9a_{n-2}

, with initial conditions

a_0 = 1

and

a_1 = 6

? [10]

Define function. Let

f_1

and

f_2

be function from R to R such that

f_1(x) = x^2

and

f_2(x) = x - x^2

. What are the functions

f_1 + f_2

and

f_1 * f_2

? [5]

What is congruent modulo? Determine whether 37 is congruent to 3 modulo 7 and whether -29 is congruent to 5 modulo 17. [5]

Give an example of tautology and contradiction. Show that implication and contrapositive are equivalence. [5]

What is direct proof? Give a direct proof that if m and n are both perfect squares, then mn is also a perfect square. [5]

What is shortest path problem? Use Dijkstra's shortest path algorithm to find the shortest path between vertices a and z in the weighted graph below: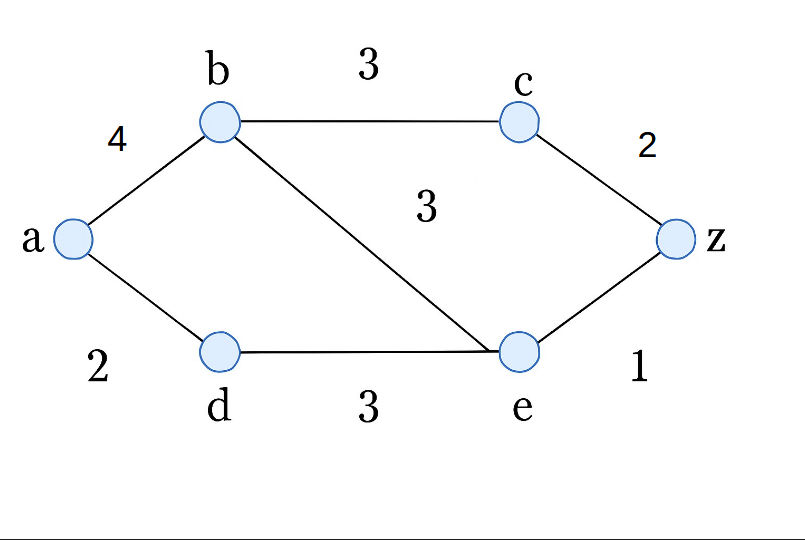

[10]

Let us assume that R be a relation on the set of ordered pair of positive integers such that

((a, b), (c, d)) \in R

if and only if ad = bc. Is R an equivalence relation? [5]

Define network flow with example. What are saturated edge, unsaturated edge and slack value? [5]

Explain the matrix representation of relations with example. [5]