State pigeonhole principle. Solve the recurrence relation $a_n = 5a_{n-1} - 6a_{n-2}$, with initial conditions $a_1 = 1$ and $a_2 = 3$. [10]

Explain the principle of inclusion and exclusion. How many integers from 1 to 30 are multiples of 2 or 3? [5]

Explain strong induction in detail. What is recursively defined function? Use mathematical induction to prove $7^{n+2} + 8^{2n+1} $ is divisible by 5. [10]

What is proof by contradiction? Give a proof by contradiction to show that if 3n+2 is odd then n is odd. [5]

Using Chinese remainder theorem solve the following congruences.x = 1 (MOD 3), x = 3 (MOD 5), x = 6 (MOD 7) [5]

Find the multiplicative inverse of 4 in $Z_{11}$ using extended euclidean algorithm. [5]

Give the example of ceiling, floor and boolean function. How do you plot the graph of the function? [5]

Express the following sentences using quantifier. 1) Not all people are loyal. 2)Everybody loves somebody. 3). Someone has passed the exam 4). Aquatic animals can't live without water 5). Some subjects are not interesting. [5]

State max flow min cut theorem. Find the value of maximal flow in the graph below: 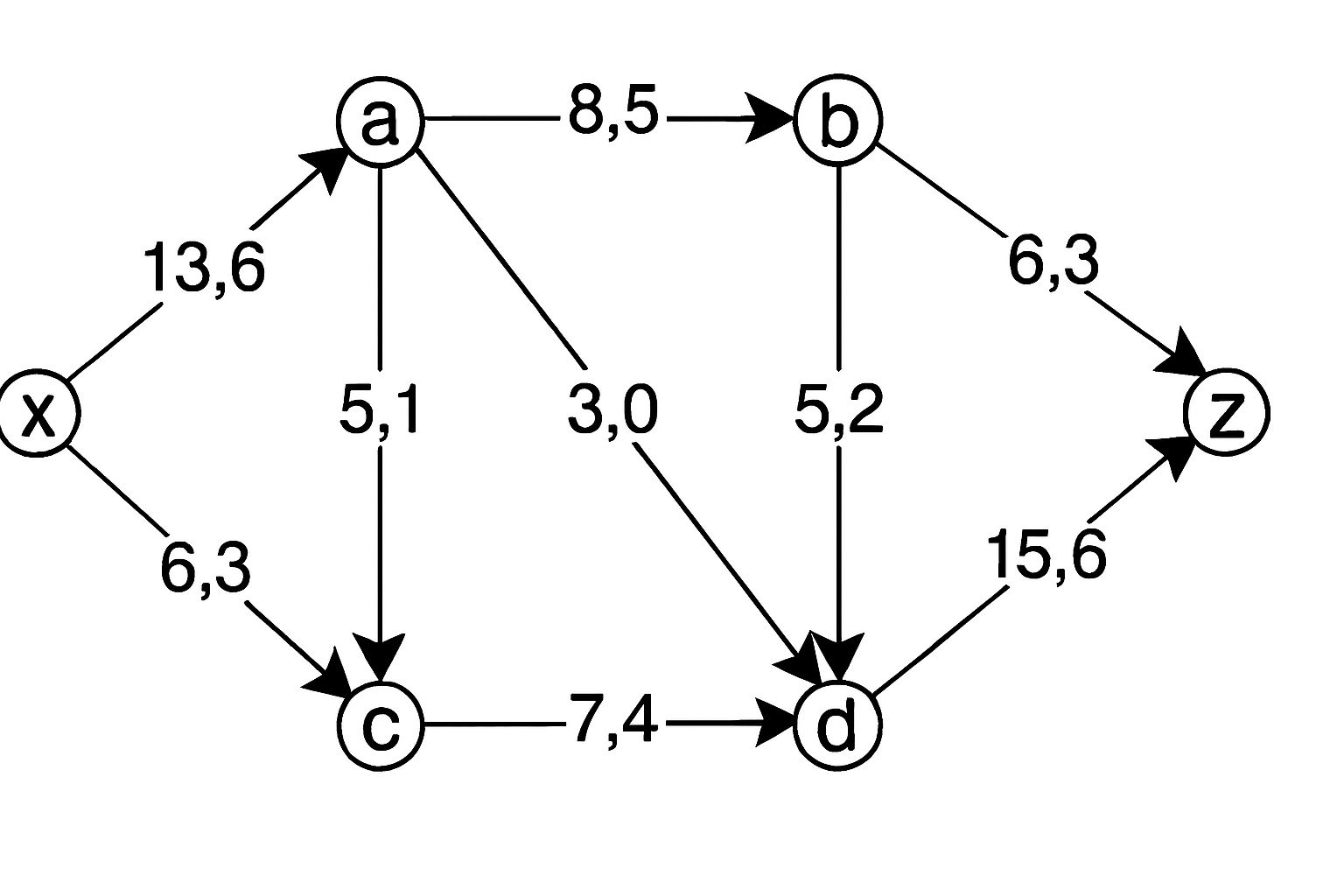[10]

State the necessary conditions for two graphs to be isomorphic. How many different words from 'MANAGER' can be generated with or without meaning? [5]

Define symmetric closure. What is the symmetric closure of the relation R = {(1,1), (1,2), (2,2), (2,3), (3,1), (2,1)} on the set A = {1,2,3}? [5]

Represent following graph using adjacency matrix. 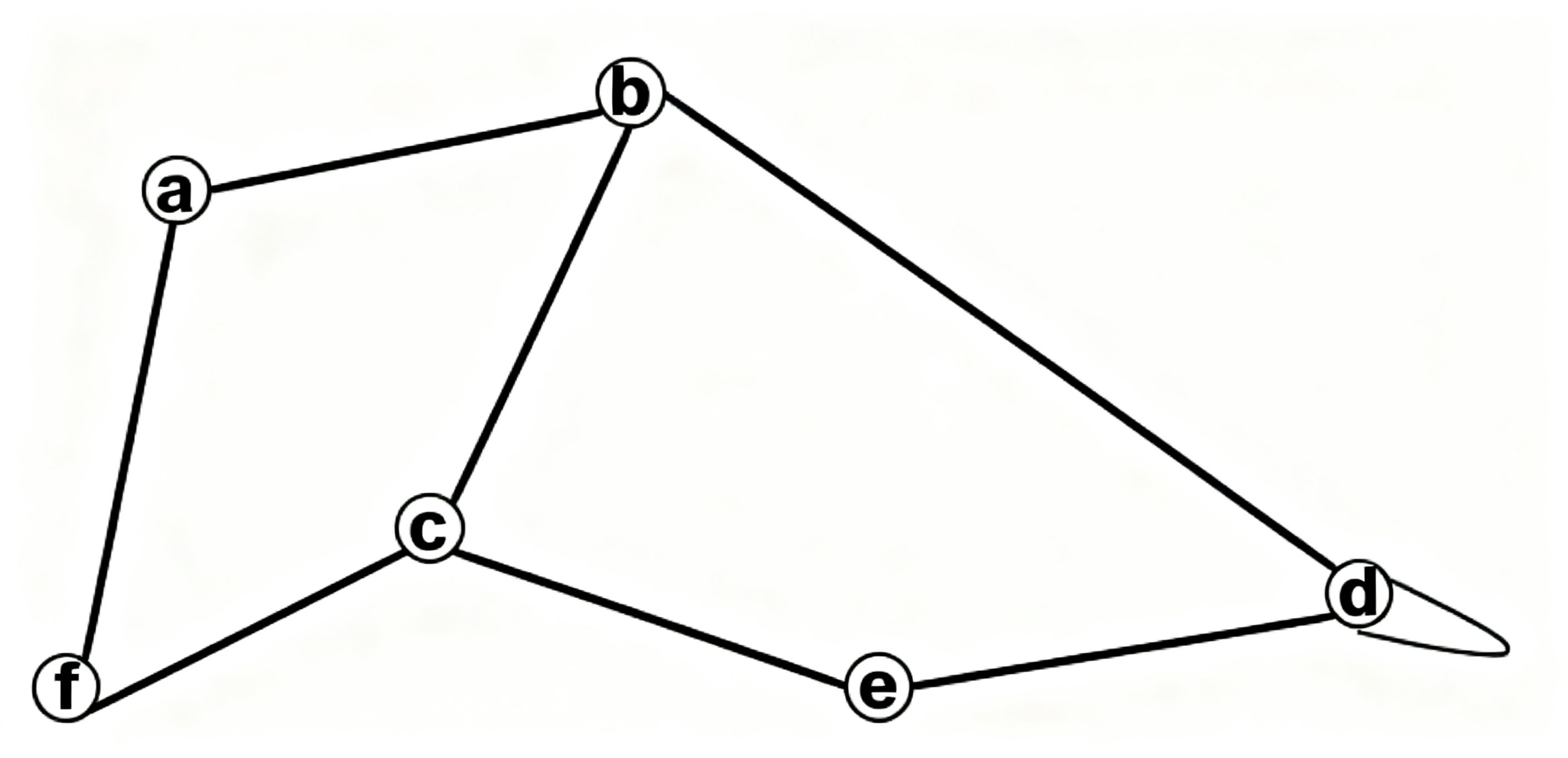[5]